Conférence sur le boulier chinois, Suanpan, le 25 novembre 2020, Institut Confucius de Pau
Le boulier chinois, Suanpan
Une nouvelle approche psychopédagogique de la construction des bases des mathématiques : le boulier chinois, antique instrument de calcul des marchands, est utilisé comme boulier didactique, dans la représentation du nombre et des calculs lors des premiers apprentissages des écoliers, ceci en préparation du calcul mental.
Les liens :
Enregistrement de la conférence https://youtu.be/EppugS-x2_w
Le diaporama de présentation https://www.editions-abacus.com/wp-content/uploads/2020/11/Conference-Confucius.pdf
L’institut Confucius de Pau https://www.icpp.fr/
Objectifs
Informer les parents, les enseignants, les enfants, les membres de la communauté culturelle chinoise sur l’intérêt pédagogique du boulier pour les écoliers en présentant :
|
Résumé du diaporama de la Conférence Confucius
| Le boulier chinois Suanpan date du début du XIIIème siècle ; Il prend la suite de différents abaques, créés par les civilisations de la Vallée de l’Indus, de Mésopotamie, d’Egypte, de Rome, de Chine, etc.
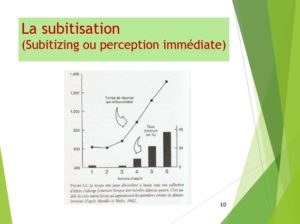
C’est un instrument de calcul pour les fonctionnaires, pour les marchands, etc. Bien sûr, aujourd’hui, avec l’informatique et l’électronique, il n’a plus aucune utilité dans ce cadre-là. Mais son rôle dans la pédagogie des mathématiques est largement oublié ou ignoré : Le modèle d’apprentissage ‘Transition -Généralisation-Représentation’, que nous avons développé pour la construction « logico-arithmétique », s’applique parfaitement au boulier vu sous l’angle « outil mathématique ». Le boulier est un générateur d’images mentales stables qui vont s’ancrer définitivement grâce à la mémoire procédurale. Enfin, la « subitisation » est rarement prise en compte dans l’enseignement des bases de la numération et du calcul aux enfants du XXIème siècle ; cependant, de façon empirique cette caractéristique du cerveau a été prise en compte dans les deux systèmes de numération connus et utilisés, décimal et sexagésimal. La première mesure scientifique, sur le sujet, date de 1982. Nous présentons 1/la numération, 2/l’addition, 3/la soustraction en établissant un parallèle entre le boulier, le calcul posé et le calcul mental. |
Bibliographie |
Etude sur le boulier:
http://revue.sesamath.net/spip.php?article639
Voir la bibliographie complète (bas de page) :
https://e-numerisme.fr/2018/05/10/notre-recherche/
Lire la revue de presse:
https://e-numerisme.fr/2018/03/14/qui-sommes-nous/
Le plan de la conférence
1/ Présentation : L’association et le modèle pédagogique développé (10 minutes)
Création de l’association en 2009. Les raisons ? Polémique sémantique, Dyscalculie ou Innumérisme ? L’étude publiée en juin 2009, tranche: il n’y a pas de dysfonctionnement, et en 2011 l’Education Nationale adopte notre point de vue, les difficultés en maths caractérisent l’Innumérisme
Notre modèle psychopédagogique constructiviste TGR (Transition-Généralisation-Représentation), bâti avec Piaget (l’abstraction réfléchissante) et Vygotski (la pensée verbale)

La stabilité des images en mémoire, selon l’expérimentation de Fahrenfort (2012), nécessite des précautions pédagogiques
Le nombre, les calculs, les maths, aujourd’hui, est-ce une construction abstraite ?
L’image technique première, corde à 13 nœuds, vilebrequin, …
La perception immédiate des quantités 1 2 et 3, la subitisation est notre hypothèse de travail
La construction mathématique passe par le socle des notions spontanées, dont la subitisation
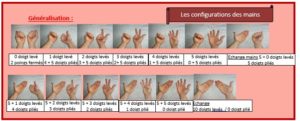
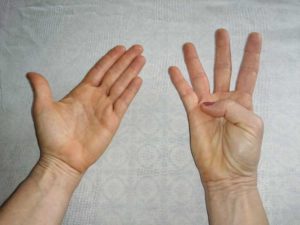
2/ Les mains ( 5 minutes)
La représentation des nombres avec les phalanges, les doigts, les mains se prolonge naturellement avec le boulier
3/ Le boulier Suanpan et les autres bouliers ( 5 minutes )
Le système positionnel décimal au boulier Suanpan
Les opérations au boulier Suanpan
Le calcul mental préparé par le boulier
4/ Le Suanpan et la numération ( 5 minutes )
Le boulier originel
Le boulier didactique permet de présenter la numération de Condorcet
5/ Le Suanpan et l’addition (10 minutes)
Exemple 1 : sans retenue addition au boulier addition posée calcul mental
36 + 13 = ?
Exemple 2 : avec retenue addition au boulier addition posée calcul mental
367 + 78 = ?
Exemple 3 : avec retenue addition au boulier addition posée calcul mental
746 + 258 = ?
Exemple 4 : avec retenue addition au boulier addition posée calcul mental
89 + 63 = ?
Exemple 5 : suite d’additions additions au boulier addition posée calcul mental
58 + 79 + 75 + 42 + 98 + 52 = ?
6/ Le Suanpan et l’addition à trou ( 10 minutes)
Exemple 1 : addition au boulier addition posée calcul mental
334 + ? = 1000
7/ Le Suanpan et la soustraction ( 10 minutes )
Exemple 1 : sans retenue soustraction au boulier soustraction posée calcul mental
287 – 34 = ?
Exemple 2 : avec retenue soustraction au boulier soustraction posée calcul mental
357 – 188 = ?
8/ Le Suanpan et la multiplication / division ( 2 minutes )
Lors d’une prochaine séance
La multiplication peut s’effectuer comme dans l’opération posée, mais habituellement on procède comme en calcul mental, en utilisant la distributivité
9/ Exercices à faire pour la prochaine conférence du 12 décembre
Exemples : sans retenue addition au boulier addition posée calcul mental
19 + 30 = ? 15 + 63 = ? 28 + 21 = ?
Exemples : avec retenue addition au boulier addition posée calcul mental
45 + 77 = ? 27 + 78 = ? 390 + 831 = ? 568 + 481 = ? 618 + 233 = ?
537,66 + 243,29 = ? 758,74 + 306,27 = ? 446,64 + 213,05 = ? 849,46 + 214,42 = ?
Exemples : sans retenue soustraction au boulier soustraction posée calcul mental
97 – 14 = ? 88 – 17 = ? 53 – 11 = ? 377 – 143 = ? 869,28 – 43,25 = ?
Exemples : avec retenue soustraction au boulier soustraction posée calcul mental
918 – 467 = ? 967 – 886 = ? 910 – 497 = ? 774,67 – 66,16 = ? 917,87 – 66,64 = ?
Série d’addition additions au boulier calcul mental
544 + 445 + 811 + 611 + 940 = ?
87 + 73 + 27 + 81 + 81 + 97 + 92 + 26 + 92 +26 +16 +67 +66 = ?
714,38 + 515,78 + 156,24 + 854, 09 + 674,29 = ?